There are many situations you might find yourself needing to have a basic grasp of how to subtract hexadecimal numbers. If you work in technical fields such as hardware and software development, hexadecimal plays a key role in computer systems and is commonly used in contexts like memory addressing, colour representations, checksums for data integrity, firmware and circuit design and in lots of data storage systems. If you deal with any of these systems it would be wise to be on top of basic hexadecimal mathematical operations.
Hexadecimal subtraction follows a similar process to decimal subtraction that you likely learned in school. There are some obvious intricacies that you should be aware of to help you subtract hexadecimal numbers efficiently.
Hexadecimal subtraction rules
Step by step hex subtraction process
Step 1: Align the numbers. In this process align the numbers by the rightmost digit. Step 2: Perform the subtraction digit by digit from right to left. First in the units place (1s) then the 16s place, the 256s place and so on. Step 3: Combine the result from each column.
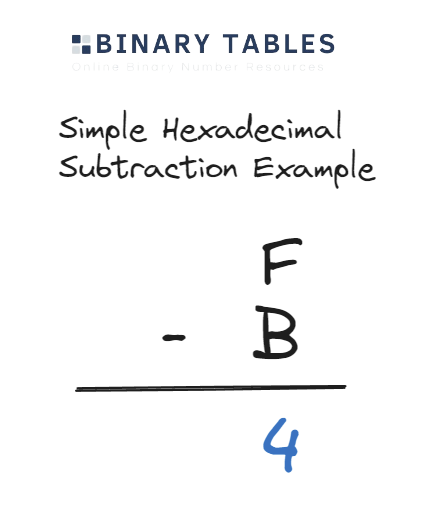
Follow this simple worked example to subtract F - B.
Follow this worked example to subtract 17F - 13.

Follow this worked example to subtract FF2 - FFF.

Hexadecimal can be represented in negative numbers and can be done so in a variety of ways. The most common way is using Two’s Complement. To do this, for each digit subtract 15 (or F) from each digit and add 1. This is what is used to store numbers in computer systems. The other commonly used system is simply using signed numbers where you use a negative sign before the number.
This quick refrence table can be used to learn to subtract hexadecimal numbers.
| - | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | F | E | D | C | B | A | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 1 | 1 | 0 | F | E | D | C | B | A | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 |
| 2 | 2 | 1 | 0 | F | E | D | C | B | A | 9 | 8 | 7 | 6 | 5 | 4 | 3 |
| 3 | 3 | 2 | 1 | 0 | F | E | D | C | B | A | 9 | 8 | 7 | 6 | 5 | 4 |
| 4 | 4 | 3 | 2 | 1 | 0 | F | E | D | C | B | A | 9 | 8 | 7 | 6 | 5 |
| 5 | 5 | 4 | 3 | 2 | 1 | 0 | F | E | D | C | B | A | 9 | 8 | 7 | 6 |
| 6 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | F | E | D | C | B | A | 9 | 8 | 7 |
| 7 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | F | E | D | C | B | A | 9 | 8 |
| 8 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | F | E | D | C | B | A | 9 |
| 9 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | F | E | D | C | B | A |
| A | A | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | F | E | D | C | B |
| B | B | A | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | F | E | D | C |
| C | C | B | A | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | F | E | D |
| D | D | C | B | A | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | F | E |
| E | E | D | C | B | A | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | F |
| F | F | E | D | C | B | A | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Decimal Subtraction | Decimal Result | Hexadecimal Subtraction | Hexadecimal Result |
|---|---|---|---|
| 10 - 4 | 6 | A - 4 | 6 |
| 15 - 7 | 8 | F - 7 | 8 |
| 20 - 5 | 15 | 14 - 5 | A |
| 16 - 10 | 6 | 10 - A | 6 |
| 14 - 6 | 8 | E - 6 | 8 |
| 12 - 9 | 3 | C - 9 | 3 |
| 5 - 1 | 4 | 5 - 1 | 4 |
| 1 - 1 | 0 | 1 - 1 | 0 |
Hexadecimal arithmetic can be performed for addition, multiplication, divisions and subtraction. Binary Tables has calculators for each of these which you can find below in the related tools.