| Binary | Hex |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| Binary | Hex |
|---|---|
| 1000 | 8 |
| 1001 | 9 |
| 1010 | a |
| 1011 | b |
| 1100 | c |
| 1101 | d |
| 1110 | e |
| 1111 | f |
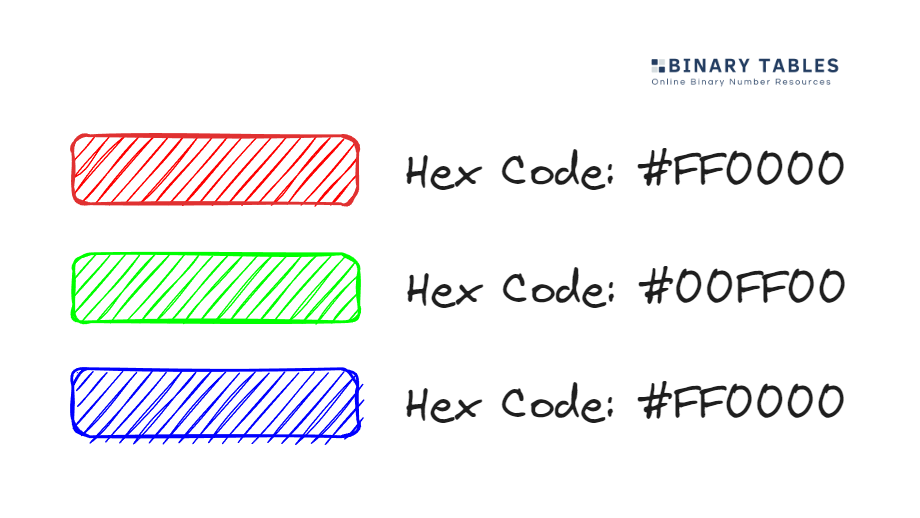
Using our free binary to hex table is easy. The table contains binary numbers from 0 to 15. In the corresponding column to the right of this number, the hexadecimal number can be found. For more complex binary hex conversions that are not covered by this table try our binary hex converter.
The hexadecimal number system (or hex number system) is a base 16 number system. This means that the system has 16 unique symbols or digits. In the case of the hexadecimal system, these include a mix of digits and letters (0 to 9 and A to F).
The below image summarizes how these hexadecimal represent decimal number values that we are more familiar with:
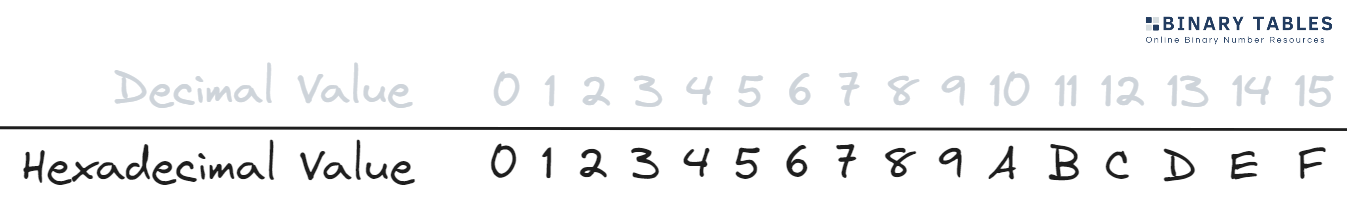
The hexadecimal number system is often used in computer and programming systems and contexts as an efficient way to represent binary numbers.
Hexadecimal representation of numbers is widely used as it offers a compromise between machine and memory efficiency while maintaining some level of human readability and comprehension.
One of the main advantages of hexadecimal over binary is that each digit represents four bits in a binary string. For example, in binary, if I wanted to represent the number eight (1000 in binary) then I could do this simply as 8 in hex. Furthermore, if I wanted to represent the number 12 in binary I would do so as 1100, whereas in hex it would just be the alphanumeric character C.
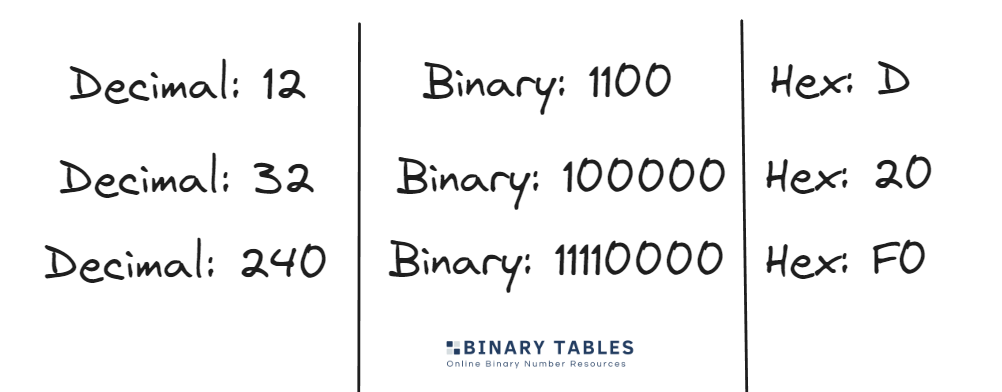
Hexadecimal is commonly used in programming for graphics and web development. Colors are often denoted in hexadecimal as each color channel in a RGB can be represented in just two characters. This means that a six-digit hex code (in the format #RRGGBB) can represent 16,777,216 color combinations available.