Binary is the base 2 number system. Unlike the decimal system (base 10) binary numbers only have 2 digits. These digits are 1 and 0. In the binary system, the digits 1 and 0 (or on and off, true or false) are used to represent every number in existence.
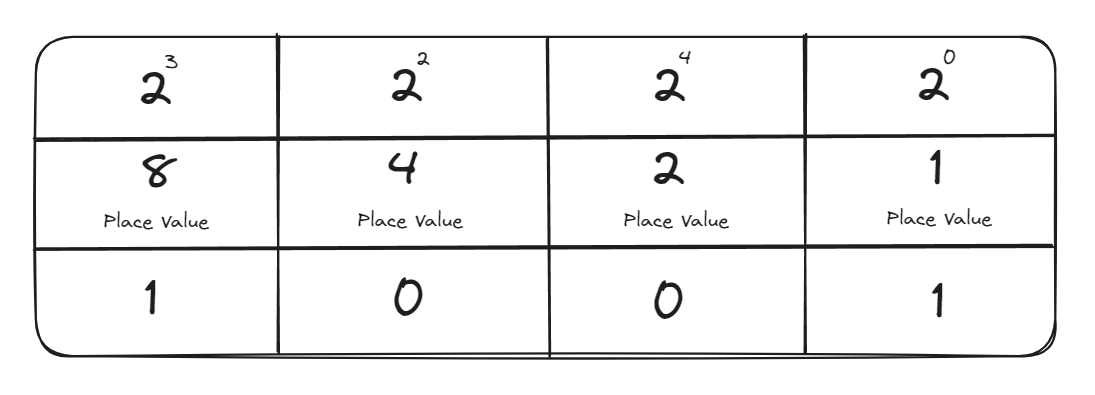
In a binary string, the place value of each digit increases by a factor of two. This can be seen in the image below which demonstrates the first 4 place values in the binary number system for the decimal number 9 (1001) in binary.
The invention of the modern binary system is generally attributed to the German mathematician Gottfried Leibniz (1646-1716) who also discovered calculus (also independently developed by Issac Newton around the same time). The mathematicians Thomas Harriot and Juan Caramuel y Lobkowitz also researched the concept of the binary number system around the same time.
However, the roots of the binary number system can be traced back further to ancient Egypt and China. The Horus-Eye fractions found in Egyptian scribes are argued by some mathematical historians to be a binary number system used to count fractional quantities of grain. Furthermore, ancient Egyptian multiplication techniques use binary representations of numbers to complete multiplication problems. In the 9th century BC China binary notation can be found in the I Ching which is built on a system of what are three-bit and six-bit binary numerals. Other traces of binary can be found in India, Africa French Polynesia, and in the languages of Indigenous Australians.
Mordern binary number systems first came into mathamatical acedmica in Leibniz’s 1703 paper the Explication de l’Arithmétique Binaire (Explanation of Binary Arithmetic). Leibniz had become an expert in the I Ching while he was in China as a missionary. While Leibniz viewed binary numbers in a theological sense as a way to explain creation out of nothing in Christianity his work paved the way for his contemporary colleagues such as Gottlob Frege and George Boole.
George Boole (British Mathematician 1815-1864) was the inverter of Boolean algebra. The idea of a boolean variable (true/false) derives from this and his name. Boolean algebra is an algebraic system of logic based on a set of truth variables (variables that can either be true/false). Boolean algebra is the core fundamental concept of binary logic which drives the digital age we live in today (this website you are reading wouldn’t be possible with binary logic or boolean algebra).
In 1937, the American mathematician and computer scientist Claude Shannon produced a set of relays and switches that formed the basis of the first digital circuit. These relays implemented binary arithmetic and Boolean algebra and formed the basis for future innovations like binary adders and complex number computers. With this, the first ever computer (The Z1 computer built by Konrad Zuse) was eventually developed around 1938.

Binary is used in lots of places, to simplify it we can break it down into four major use cases. These include the use of binary in computer systems, storage and memory, programming languages and communications. Let’s go into a little bit of detail about how they are used in each area.
The primary use of binary is seen in computer systems. Everything “digital” can be fundamentally attributed to binary as it is somewhere in the system represented by 1s and 0s in relays and switches.
All digital circuits are built with logic gates (AND, OR, NOT, NAND, NOR gates). Combined these can perform complex calculations based on binary inputs (1s and 0s). The main think tank of a computer (or mobile phone) the CPI is built with logic gates that control, sort, control and perform arithmetic on binary inputs. Given this computer systems and components (memory, processors, storage and buses) are designed around binary principles to ensure the efficiently work with binary signals in inputs.
Given computer systems work with binary signals in inputs, it is natural that data is also stored in binary form at its simplest layer. The smallest unit of the digital storage system the bit is used to represent a single binary digit (1 or 0). 8 bits make a byte which can be used to represent an ASCII character.
The storage capacity of computer systems is given based on the amount of binary data it can store. from 8 bits we can form 1 byte and from 8 bytes we can form 1 kilobyte and so on.
Many forms of binary encoding exist. Binary encoding is a way to map binary to another system. For example, text can be mapped to and from binary with ASCII. International characters can be represented in alternative character representation systems like Unicode. Other formats more suitable for other media systems are also used.
Programming languages are used to create instruction sets for computers. While at a high level programming languages are written in a way that humans can comprehend and understand these are ultimately compiled down to a set of machine code instructions that the computer can execute. Code may go through a few sets of compilation to reach binary depending on how high level the code is. Low-level programming languages like Assembly, Ada, and C will compile quicker with binary than high-level languages like Java, Python and Javascript which require more steps to become machine-readable code.
Programming languages also utilise binary to perform operations such as binary logic and arithmetic, represent data, and read input and output to ensure things are efficient.
The final major use for binary is in communications systems. Digital signals transmit using binary to communicate data between different systems. One of the most common uses for this is in networking. The TCP/IP networking protocol uses binary headers to encapsulate and transmit data packets over a network and between computers and servers.
Binary mathematics and arithmetic operations are useful to gain a full understanding of how computer systems and programming algorithms manipulate binary to perform complex operations and solve large mathematics problems efficiently.
Like decimal or any number system, the four basic mathematical operations; addition, subtraction, multiplication and division can be performed in binary. In places, these are similar to decimal operations, for example, 1 + 1 in binary equals 10 (2) and 1 - 1 in binary equals 0. Binary multiplication and division can be more complex. To practise binary mathematics try our free binary calculators below:
The biggest advantage of the binary number system is its ability to be used in digital and computer systems as highlighted above. The simplicity of binary makes it useful to be easily stored, transformed, used in logic and maths and easily transmitted. This makes binary something that while not everyone is aware of is used by almost everyone on the planet in their everyday life.
While binary is perfect for digital systems it is hard for humans to understand without significant training and time to sit down and work out. Binary is also not super efficient for storing large numbers. In these cases, number systems like hexadecimal, octal or decimal are much more efficient. Finally binary can be inefficient for performing certain mathematical operations with real or complex numbers where computations require a large overhead and precision is important.
Binary is the foundation of the digital systems we use in our daily lives. It is the backbone for all the processing, storage, communication and computational systems that are a pivotal part of our lives in this information era. As a computer scientist, mathematician, and technician. programmer or anyone working in the digital space it is important to understand. This article gives a brief overview of binary to help you get started on your binary learning journey.
Continue your binary learning journey with our free resources below: